線性代數：各大 LLM 模型背後的數學魔法

在 AI 世界裡，「數學是萬物語言」這句話絕非空談。從圖像辨識、語音辨識到自動駕駛，背後都藏著一門經典卻強大的數學學科：線性代數。這門來自課本裡的知識，正默默成為 AI 革命的核心動力。

電腦眼中的世界：一切都是矩陣與向量

當我們看到一張貓的照片時，所感受到的是牠的毛色、表情，甚至是可愛的姿態；但對電腦而言，這張圖片的本質卻是一組龐大的數字資料。電腦在儲存圖像時，會將畫面拆解為無數個像素（Pixel），每個像素代表圖片上的一個小點。這些像素進一步被分解為 RGB 三原色的數值，也就是紅（Red）、綠（Green）、藍（Blue）三種色彩的強度。每一個顏色強度的數值通常介於 0 到 255 之間，形成一組三維的色彩資訊。

這些數值並非隨機散落，而是依照像素在圖片中的位置，整齊地排列成行與列，最終形成一個或多個矩陣（灰階圖片為單一矩陣，彩色圖片則對應三個矩陣）。對於電腦來說，這樣的矩陣就成為它「看見」與「理解」圖像的基礎形式。

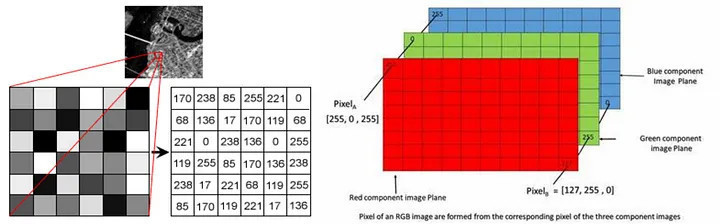
不只圖像如此，文字、聲音、使用者行為……等，其實都可以轉換為「矩陣」的形式: 例如: 文字資料 可以透過詞嵌入技術（Word Embedding），將每個單詞轉換成固定長度的向量，進一步組合成矩陣，讓模型能處理句子、段落甚至整篇文章的語意關係。

向量與矩陣：每個 AI 模型都離不開的基礎結構

當這些來自圖像、文字、聲音或使用者行為的資料被轉換為矩陣與向量後，AI 模型就能正式開始「運作」。以神經網路為例，這些數據會作為輸入，進入模型的第一層，並與該層的權重矩陣進行矩陣乘法，再加上偏置向量，最後通過激活函數進行非線性轉換。這樣的運算會在每一層中不斷重複，資料也隨之一步步被轉換成更抽象、更有意義的特徵表示。

以圖像識別為例，初始幾層可能僅僅辨識出簡單的邊緣與形狀，而中間層則會開始辨識出眼睛、耳朵等具體部位，直到最後輸出層做出「這是一隻貓」的判斷；在處理文字時，模型會從向量中辨識出語意結構與上下文關係，最終推斷出句子的情感或主旨。

不論輸入是什麼樣的資料類型，這些計算本質上都依賴線性代數所提供的運算工具——矩陣乘法、向量加總、點積等。這讓 AI 模型能夠用統一的數學語言，處理來自現實世界的各式資料，進而實現分類、預測、生成等功能。可以說，線性代數不只是 AI 模型的基礎結構，更是支撐整個運算過程的數學引擎。

降維與特徵值：讓 AI 精準鎖定關鍵資訊

在處理龐大資料時，AI 並不一定需要全部的特徵。事實上，過多的變數不僅會增加運算負擔，還可能導致模型過度擬合、影響預測準確性。這時，線性代數中的一項經典技術——主成分分析（Principal Component Analysis, PCA）便發揮了關鍵作用。

PCA 透過計算資料的特徵值與特徵向量，將原本高維度的數據投影到一個較低維度的空間，保留變異度最高、也就是最具資訊價值的方向。舉例來說，原本有上千個欄位的使用者行為資料，在經過 PCA 降維後，可能只剩下幾個「主成分」就足以讓模型進行有效預測。這不僅大幅減少運算時間，也能提升模型的泛化能力與穩定性。

梯度下降：驅動 AI 學習的數學引擎

其中最著名的模型應用就是梯度下降了，要讓 AI 模型具備判斷與預測能力，就必須經過不斷的訓練與調整。而這背後的核心機制，正是來自線性代數的梯度下降法（Gradient Descent）。在每一輪訓練中，模型會根據輸出的誤差，計算出損失函數對參數的偏導數，也就是所謂的梯度向量。這個向量指出了「損失最迅速下降的方向」，模型便沿著這個方向調整內部的權重與偏置。這樣的運算牽涉到大量的矩陣乘法與向量更新，並在更進階的版本中，使用如 Jacobian 或 Hessian 矩陣來加速與精準化學習過程。

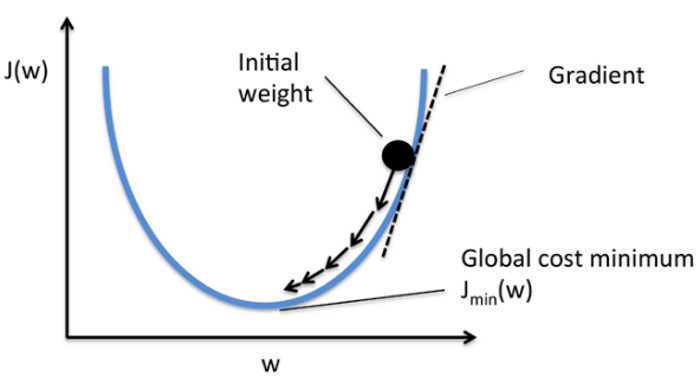
這項過程可以想像成將整個優化問題視為一座起伏不定的山谷，而我們的目標，就是找到這個谷底——也就是讓損失函數值最低的參數組合。透過梯度下降，AI 模型就像盲眼的登山者，靠著梯度這個「指南針」，一步步朝著斜率最陡峭、也就是誤差減少最快的方向前進。每一次的步伐（學習率）若拿捏得當，就能穩定地抵達最佳解。

數學的力量，讓 AI 真正聰明起來

從資料的轉換、特徵的提取，到模型的訓練與優化，線性代數無所不在。它不只是 AI 背後的輔助工具，更是驅動整個人工智慧體系前進的核心引擎。矩陣與向量讓資料得以被「看見」，特徵值幫助模型聚焦於關鍵資訊，而梯度與導數則引導模型一步步學習並接近答案。

在這個強調智慧與效率的時代，AI 能有如此驚人的表現，背後少不了數學的支撐。線性代數就像是 AI 世界中的語法與邏輯，為看似神祕的機器學習模型，提供了清晰且可解釋的運算基礎。未來的科技會變得更快、更準、更智能，而這些進步的每一步，都有數學在背後默默運作。對於想理解 AI 的人來說，線性代數，無疑是通往智慧之路的第一把鑰匙。若要理解模型背後的運作原理，線性代數是必不可少的一門學科！